In continuation of this exciting quest to learn more about data structures and algorithms. I will love to talk about binary search trees which builds on the knowledge last discussed on linked-list which is referenced from this book, you can find the post here.
Why Binary Search Trees? Link to heading
There are some data structures that allow a fast search or flexible update, but not both. An unsorted, doubly-linked lists support insertion in constant time O(1) but the search took linear time O(n) in the worse case. Sorted arrays support binary search which helps lookup in logarithm time O(logn), but at the cost of linear-time update.
Binary Search Trees will allow us to have a fast search and update in logarithm time O(logn) but there is a caveat to this which will be explained later when we talk about balancing a binary search tree.
The arrangement and balancing of the tree is done in a way that the keys of nodes on the left subtrees are less than the keys on the right subtrees and this leads to the tree being sorted always.
Implementation of Binary Search Trees Link to heading
To create a binary search tree, we need a linked list with 2 pointers per node. The idea is that there is a left subtree and right subtree and the node is labeled with a key. I will implement the following operations on the binary search tree: Searching, Traversal, and Insertion.
The nodes of the tree have 1. left pointer 2. right pointer 3. optional parent pointer 4. data field, where we store values inserted. All the code and tests for this implementation can be found here on github.
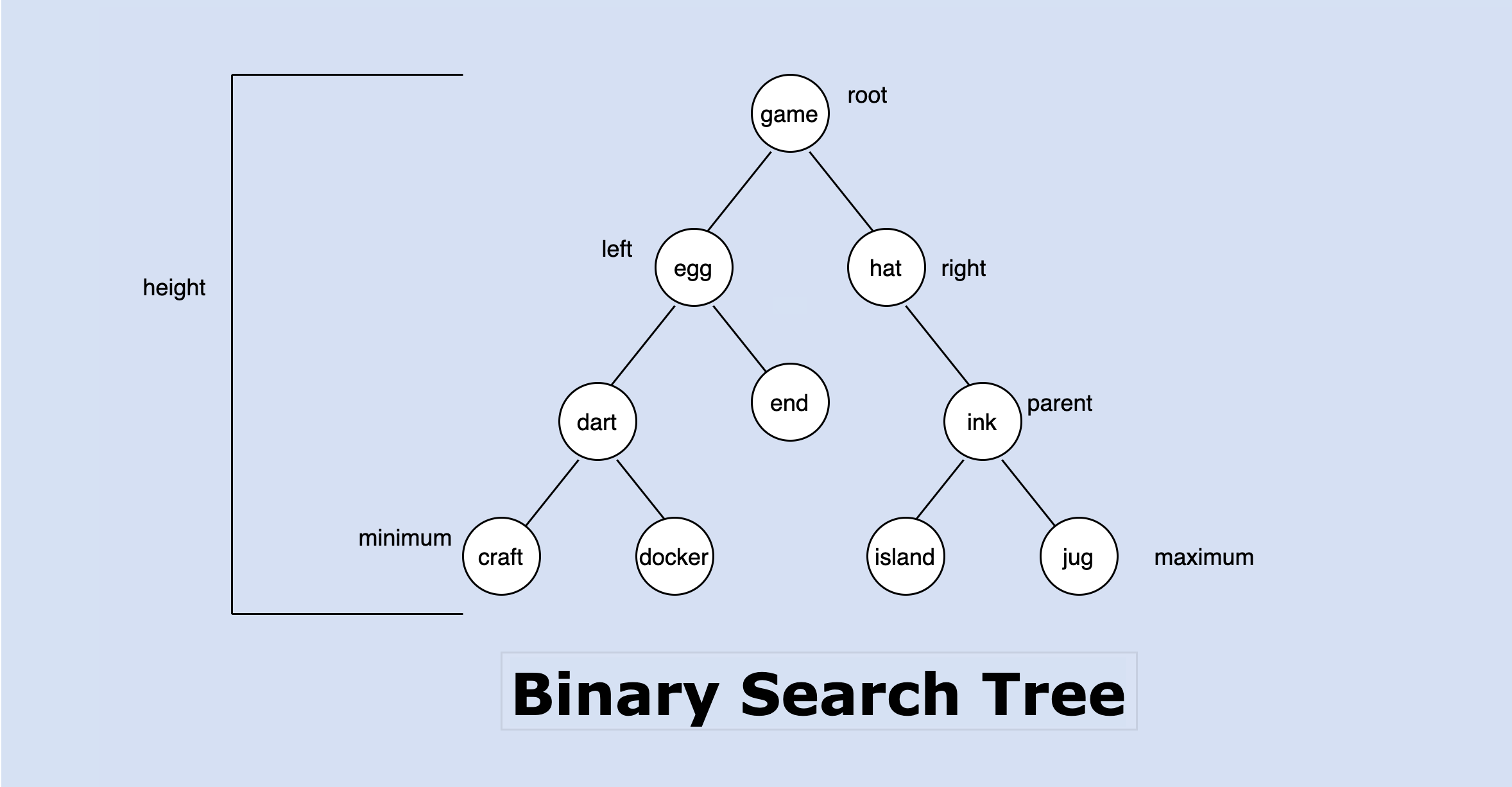
To create a binary search tree, you will need to have a root where everything builds from, it can be empty or it can consist of a node together with 2 binary search trees called left and right subtrees which consist of nodes, a node (tree) which is the smallest unit and foundation of a binary search tree as shown below:
// Tree is the basic structure or node in a binary search tree.
type Tree struct {
parent *Tree // parent can be nil i.e Root tree
left *Tree // left child or left subtree
right *Tree // right child or right subtree
Item string // data held by the node
}
The parent can be a tree but in the case of a rooted tree, it will be empty and the left and right can also be empty which indicates we are at the end of the tree. We will model a Dictionary (collection of sorted words in ascending order) using this data structure.
// BinarySearchTree to store the words of a dictionary.
type BinarySearchTree struct {
Root *Tree
}
Insertion Link to heading
I have 2 different implementations for the insertion operation, the recursive and non-recursive approach.
Non-Recursive Link to heading
This approach is more code and a bit easier to reason about. We will start going through the binary search tree from the root and then based on the item to be inserted, we have the following decision points and this also forms the concept behind the recursive approach:
If the root is empty, insert the item thereby creating a new tree, where parent, left and right subtree or children are nil.
If the item to be inserted is less than the current item in the node, we move to the left subtree and continue our search till we get to the end of the left-subtree i.e nil, then we inserted a new item there encapsulated as a new tree.
If the item to be inserted is greater than the current item in the node, repeat the above step but instead of moving to the left subtree, we move to the right subtree.
This is illustrated below:
func (bt *BinarySearchTree) NormalInsert(item string) {
if bt.Root == nil {
bt.Root = &Tree{
Item: item,
}
return
}
currentTree := bt.Root
insertionLoop:
for {
switch {
// go to the left subtree
case item < currentTree.Item:
if currentTree.left == nil { // at the end of the left subtrees
// attach the new node
currentTree.left = &Tree{
Item: item,
parent: currentTree,
}
break insertionLoop
} else {
currentTree = currentTree.left
}
break
// go to the right subtree
case item > currentTree.Item:
if currentTree.right == nil { // at the end of the right subtree
// attach the new node
currentTree.right = &Tree{
Item: item,
parent: currentTree,
}
break insertionLoop
} else {
currentTree = currentTree.right
}
break
default:
break insertionLoop
}
}
}
We needed a label on the loop because when we break in a switch statement, it breaks out of the switch and not the loop.
Recursive Link to heading
Just as discussed above, this approach is less code but takes a little to reason about especially when you get to the point where you want to attach the new tree to its parent, it follows the same approach above.
func (bt *BinarySearchTree) RecursiveInsert(currentTree **Tree, item string, parent *Tree) {
// currentTree is a pointer to the memory location(also a pointer) where the current node tree
// is stored. This is needed because, when we get to a tree that is empty and we need to insert
// the new item, we'll need to replace the empty space (which is to hold a tree) with the new tree, this warrants having access to the location.
// If you don't do this, your update will be detached from the main binary search tree.
// when we have come to the end of the search.
if *currentTree == nil {
newTree := &Tree{
Item: item,
left: nil,
right: nil,
parent: parent,
}
// Attach to its parent, by getting the memory location where the currentTree.
*currentTree = newTree
return
}
// Recursively search for where to put the item.
if item < (*currentTree).Item { // diverge to the left subtree
bt.RecursiveInsert(&(*currentTree).left, item, *currentTree)
} else {
bt.RecursiveInsert(&(*currentTree).right, item, *currentTree)
}
}
Attaching the new node to the tree takes constant time but the search operation that is performed before the node is attached uses a running time of O(h), h - the height of the tree
Note that the insertion here doesn’t guarantee a balanced search tree, this will be discussed in another post when I discuss the Red-Black Tree and Slay Tree which is guaranteed to be O(logn) in height and that applies for insertion, update, and deletion, the tree responds to mutation to make it close to being balanced to guarantee the height of the tree is always or close to O(log n).
What we have so far is a random binary search tree that is good too but if the insertion goes south (which we don’t have control over the values or items inserted by the user), we can end up in O(n) height for the tree.
Searching Link to heading
It is important to label a binary search tree so that we can uniquely identify each tree using its identifier.
These are the steps to consider when performing this operation:
- Start the search at the root of the tree
- If the search has a key to be searched for;
- Check if the key is greater or less than the key or identifier in the root, this will determine if we’ll go down the left child of the tree or the right.
- Continue these steps recursively till you find the item or get to the end of the tree
The search algorithm runs in O(h) time, where h is the height of the binary search tree
Finding the minimum node in the tree comes with the understanding that, the leftmost subtree has the minimum item, and also for maximum, the rightmost subtree has the highest item in the tree. The smallest key must reside in the left subtree of the root since all keys in the left subtree have values less than that of the root and the largest key resides in the right subtrees since the keys in the right subtrees are higher than the root. These operations are illustrated below:
Search:
// Search searches for an item, it expects to start from the Root.
func (bt *BinarySearchTree) Search(item string) string {
if result := bt.Root.Search(bt.Root, item); result != nil { // found!
return result.Item
}
return ""
}
Minimum:
func (bt *BinarySearchTree) FindMinimum() *Tree {
// start from the Root and move to the left subtrees
minTree := bt.Root
for minTree.left != nil {
minTree = minTree.left
}
return minTree
}
Maximum:
// FindMaximum returns the largest or highest item in the tree.
func (bt *BinarySearchTree) FindMaximum() *Tree {
// start from the Root and move right wards
maxTree := bt.Root
for maxTree.right != nil {
maxTree = maxTree.right
}
return maxTree
}
Traversal Link to heading
It is about visiting all the nodes in a rooted binary tree, this is a very important part of many algorithms. This is also a foundation for traversing the nodes and edges in a graph.
It comes with the understanding that the elements in the binary search tree are already sorted since the smallest keys are on the left of the root and the largest keys are on the right of the root tree.
This is achieved by using a recursive approach visiting the nodes of the tree, processing the left trees, processing the item on that tree, and also visiting the right subtrees recursively. The order in which this operation is done leads to 1. In-order traversal 2. Pre-order traversal 3. Post-order traversal
In-order traversal: Link to heading
Traverse the left subtrees, process the item and traverse the right subtrees, the index of the recursion will be when we reach the leaf or node with no children i.e left and right tree are nil.
Pre-order traversal: Link to heading
Process the item in the tree first, then Traverse the left subtrees and traverse the right subtrees
Post-order traversal: Link to heading
Traverse the left subtrees first, then traverse the right subtrees and then process the item in the tree.
Pre-order and Post-order traversal comes in handy when the binary search tree represents an arithmetic expression or a logical expression where the order of operation is very important.
The running time of traversal is linear O(n) because each item is visited once.
Below is the illustration of In-order traversal, you can get the implementation of Pre-order and Post-order on github:
In-order Traversal:
// InOrderTraversal traverse in the order [smallest ... largest] [allLeft ... allRight]
func (bt *BinarySearchTree) InOrderTraversal(t *Tree, processItem func (string)) {
if t != nil {
bt.InOrderTraversal(t.left, processItem)
// process the item in the tree using the power of closure
processItem(t.Item)
bt.InOrderTraversal(t.right, processItem)
}
}
Final Thoughts Link to heading
Picking the wrong data structure for the job can be disastrous in terms of performance. Identifying the very best data structure is usually not as critical because there can be several choices that perform similarly. - Steven S. Skiena
The problem you are trying to solve, will and should always inform the kind of data structure you use. It is a learning journey as always, I will be glad to hear from you if you have question(s) or feedback, have fun!